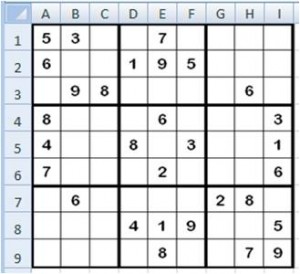
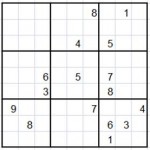
Sudoku es un rompecabezas matemático que se publicó por primera vez en el 1970 y se popularizó en Japón (1985) y en el resto del mundo (2005). Consiste en una matriz de 81 celdas ordenadas en 9×9 y con cuadriculas de 3×3. El objetivo es rellenar cada fila, columna y cuadricula con números del 1 al 9 de modo que los números no se repitan en ninguna fila ni columna. En la siguiente imagen puedes ver un SUDOKU realizado en Excel.

 

¿Cómo resolver un SUDOKU?

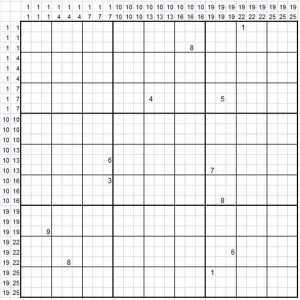
Un método de resolverlo un Sudoku es creando una matriz, esta vez de 27×27, donde escribiremos los candidatos de cada celda, o sea, las posibles soluciones para cada celda.

Para ello, por cada celda del Sudoku crearemos una macro-celda de 3×3 donde estarán todas las soluciones posibles de una celda ( del 1 al 9). A continuación iremos borrando los números que no pueden ser una solución posible, por no cumplir los criterios de que en cada cuadricula, en cada fila y en cada columna existen todos los número del 1 al 9 y además entre filas y entre las columnas no se repiten números.

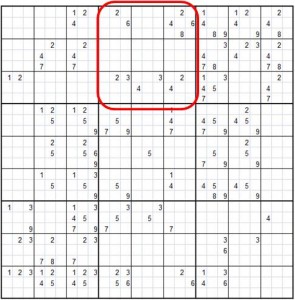
Por ejemplo en la celda B2 (señalada en la siguiente imagen) del Sudoku no pueden ser solución los números 5, 3, 6, 9 y 8 porque ya están en la cuadrícula, ni los números 6, 1, 9 y 5 porque ya están en la fila, ni los números 3, 9 y 6 porque ya están en la columna. Por tanto las soluciones posibles, o sea los candidatos, serían el 2, 4 y 7.

Las soluciones se encontrarán buscando sobre la matriz de Candidatos, los candidatos únicos y los candidatos aislados.

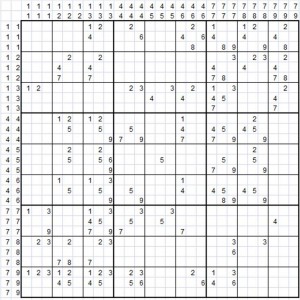
Candidatos únicos son cuando en una macro-celda solo hay un candidato, que por tanto es la solución de esa celda. Por ejemplo, en la macro-celda correspondiente a la celda E5, hay solo un 5, por lo que es la solución de la celda E5.

Candidatos aislados los llamamos cuando en las macro-celdas de una cuadricula o de una fila o de una columna, hay un número que solo aparece una vez. Ese número es la solución de la celda donde está. Por ejemplo en las macro-celdas correspondientes a las celdas D1:F3 de la matriz Sudoku, vemos que aparecen varios 2, 3, 4, y 6, pero solo un 8 en la posición F1, con lo que la solución de la celda F1 es un 8.

¿Cómo se realiza esto sólo con fórmulas en Excel?

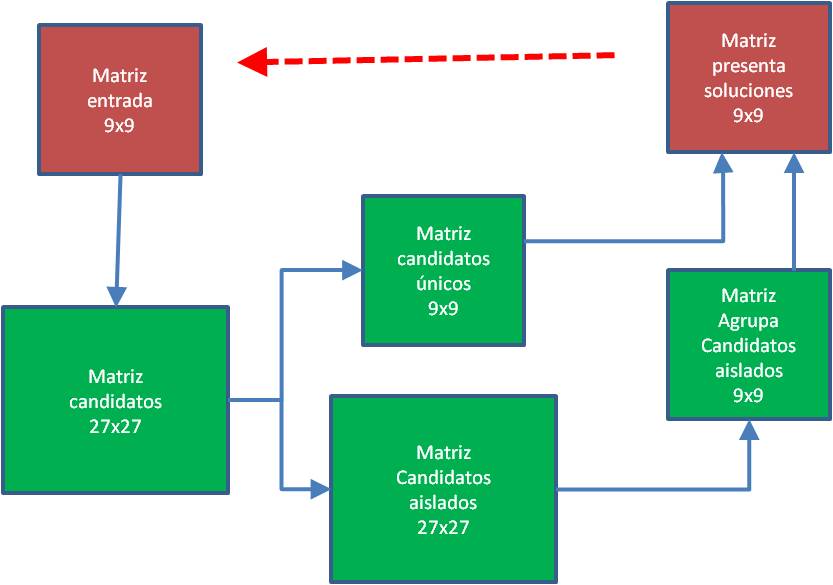
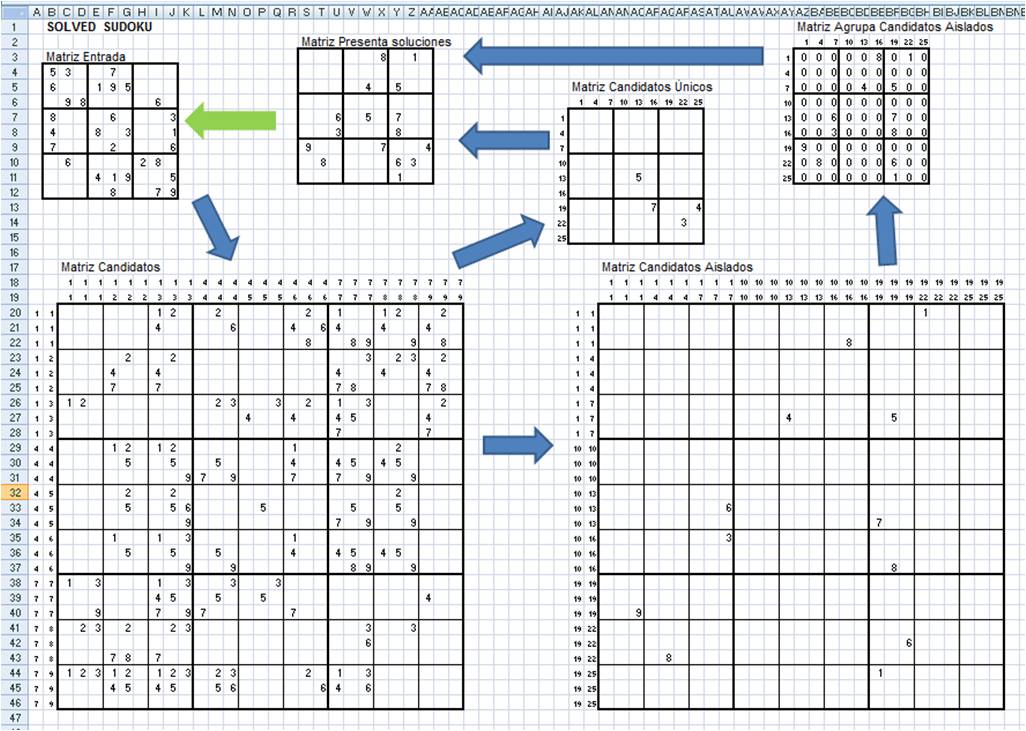
Para resolver el Sudoku vamos a montar una estructura de matrices encadenadas. Esto nos va a permitir simplificar las ecuaciones necesarias. La estructura propuesta es:

• La Matriz Entrada (9×9) es donde se trasladan los datos iniciales del Sudoku y donde se pondrán las soluciones que vayan apareciendo, hasta completar el Sudoku.
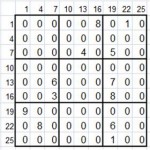
• Matriz Candidatos (27×27), partiendo de los datos de la Matriz Entrada, calcula los candidatos, en macro-celdas.
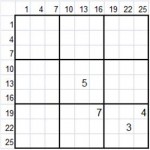
• Matriz Candidatos Aislados (27×27), partiendo de los datos de la Matriz Candidatos, se extraen los candidatos aislados.
• Matriz Agrupa Candidatos Aislados (9X9), parte de la Matriz Candidatos Aislados y se agrupan en 9×9 los candidatos aislados.
• Matriz Candidatos Únicos (9×9), parte de Matriz de Candidatos y extrae los candidatos únicos, en una matriz de 9×9.
• Matriz Presenta Soluciones (9×9), toma las soluciones de la Matriz Candidatos Únicos y de Matriz Agrupa Candidatos Aislados, las agrupa y las presenta.
• Cada matriz se basa en los datos de la anterior en modo cascada con lo que se reducen y simplifican las ecuaciones.
• Las soluciones aportadas en la Matriz Presenta Soluciones se pasan a la Matriz Entrada de modo manual, con lo que cada vez que se añade un valor se vuelven a calcular todas las matrices.

Matriz Candidatos

Cada Celda de la Matriz Entrada tiene asociada una macro-celda de la Matriz Candidatos, donde están los candidatos del 1 al 9. Con lo que cada una de las celdas de una misma macro-celda tiene asociada la misma celda de la Matriz Entrada.

Para cada celda de la macro-celda, que representa un número Z, se siguen los siguientes criterios:

 

Utilizamos las funciones:

• SI (prueba lógica; valor si verdadero; valor si falso), para la opciones
• DESREF (Ref, filas, columnas, alto, ancho), para poder, desde una celda de una macro-celda de la Matriz Candidatos, referenciar una celda o una cuadrícula o una fila o una columna de la Matriz Entrada.
• CONTAR.SI (rango,criterio), para comprobar que existe un Z en una cuadrícula, fila o columna. Rango será el de cuadrícula, fila o columna y criterio será Z. El resultado de la función será 1 si existe y 0 si no existe.

 

La función DESREF selecciona un rango de un numero de filas indicado por alto y un número de columnas indicado por ancho, situado a un número de filas indicado por filas, y a un número de columnas  indicado por columnas, a partir de una celda de referencia, indicada por Ref.

Para identificar la celda, la cuadrícula, la fila y la columna que corresponde a cada celda de la Matriz de Candidatos, se utilizan unos punteros en los extremos de filas y columnas de la matriz, con el siguiente significado:

• Pf, Pc: punteros de fila y columna de la celda de la Matriz Entrada relacionada.
• Pfc,Pcc : puntero de fila y columna de la cuadrícula de la Matriz Entrada relacionada.

La ecuación para cada celda de la matriz Candidatos sería:

= SI(DESREF(Ref_ME;Pf;Pc)=””; SI(CONTAR.SI(DESREF(Ref_ME;Pfc;Pcc,3,3);Z)=1;” “;
SI(CONTAR.SI(DESREF(Ref_ME;Pf;1,1,9);Z)=1;” “;
SI(CONTAR.SI(DESREF(Ref_ME;1,Pc,9,1);Z)=1;” “;Z)));” ”)

Donde:

• Ref_ME, representa la referencia de la Matriz Entrada, en la esquina externa superior izquierda.
• Pf, Pc: punteros de fila y columna de la celda de la Matriz Entrada relacionada.
• Pfc,Pcc : puntero de fila y columna de la cuadrícula de la Matriz Entrada relacionada.

Los valores de los punteros serían:

 

Matriz Candidatos Aislados

Es una matriz del mismo tamaño que Matriz Candidatos (27×27) y done se van a extraer los candidatos aislados desde la matriz Candidatos, o sea, los candidatos que son únicos en una cuadrícula, una fila o una columna. Igualmente contendrá macro-celdas con los número posibles del 1 al 9.

Los criterios que se siguen, para una celda de número Z , son:

 

Para referenciar a una celda, una cuadrícula de macro-celdas (9×9), una fila de macro-celdas (3×27) o una columna de macro-celdas (27×3), vamos a utilizar la función DESREF (), ya comentada.

Para ver si existe un solo número en un rango utilizaremos la función CONTAR.SI ()

Para gestionan las opciones utilizamos la función SI ()

Para identificar la celda, la cuadrícula, la fila y la columna que corresponde a cada celda de la Matriz de Candidatos Aislados, se utilizan unos punteros en los extremos de filas y columnas de la matriz, con el siguiente significado:

• Pf, Pc: punteros de fila y columna de la celda de la Matriz Candidatos relacionada.
• Pfc,Pcc : puntero de fila y columna de la cuadrícula de la Matriz Candidatos relacionada

La ecuación para cada celda NX de la Matriz Candidatos Aislados, correspondiente a un número Z, es:

= SI(NX<>” ”; SI(CONTAR.SI(DESREF(Ref_ME;1;Pc,27,3); Z)=1;Z;
SI(CONTAR.SI(DESREF(Ref_ME;Pfc;Pcc,9,9);Z)=1;Z;
SI(CONTAR.SI(DESREF(Ref_ME;Pf,1,3,27);Z)=1;Z;” “)));” ”)
Donde:

• Ref_ME, representa la referencia de la Matriz Candidatos, en la esquina externa superior izquierda.
• Pf, Pc: punteros de fila y columna de la celda de la Matriz Candidatos relacionada.
• Pfc,Pcc : puntero de fila y columna de la cuadrícula de la Matriz Candidatos relacionada.

Los valores de los punteros serían:

 

Matriz Agrupa Candidatos Aislados

El objetivo de esta matriz es pasar a una matriz de 9×9 los candidatos aislados identificados en la Matriz Candidatos Aislados. El criterio es agrupar cada macro-celda en una celda. Cada macro-celda puede tener todas sus celdas en blanco o solo una de sus celdas con algún valor.

El criterio, para cada celda, es: Sumar macro-celda

• Utilizamos la función SUMA (rango), donde rango es cada macro-celda.
• Para identificar las macro-celdas utilizaremos la función DESREF
• Para identificar la posición de la macro-celda dentro de la Matriz utilizamos unos punteros, que colocamos en los bordes externos de filas y columnas.

La ecuación es:

=SUMA(DEREF(Ref;Pf;Pc;3,3)

Donde

• Ref: Referencia en la esquina externa superior izquierda de la Matriz Candidatos Aislado
• Pf,Pc: puntero fila y columna, en los bordes de la Matriz Agrupa Candidatos Aislados.
• Los datos de la matriz, al ser resultados de una SUMA, son numérico.

Los valores de los punteros serían:

Matriz Candidatos Únicos

Esta matriz extrae de la Matriz Candidatos las soluciones de candidatos únicos, que son cuando en una macro-celda solo hay un candidato. Los criterios para esta matriz son:

Si Solo existe un candidato en la macro-celda =>> Entonces Poner ese valor ==>Sino   Poner blanco

Utilizaremos las funciones:

• CONTAR, para comprobar que solo existe un candidato en la macro-celda.
• DESREF, para seleccionar el rango de una macro-celda
• SUMA, para identificar el valor del candidato.
• SI, para las opciones
• Para identificar una macro-celda utilizaremos punteros en los bordes externos de filas y columnas.

La ecuación sería:

= SI(CONTAR(DESREF(Ref;Pf;Pc;3;3))=1;SUMA(DESREF(Ref;Pf;Pc;3;3));” “)

Donde:

• Ref: Referencia en la esquina externa superior izquierda de la Matriz Candidatos
• Pf,Pc: puntero fila y columna, en los bordes de la Matriz Candidatos Únicos.

Los valores de los punteros serían:

Matriz Presenta Soluciones

Es la matriz donde se muestran las soluciones posibles para que el usuario las traslade a la Matriz de Entrada. Toma los de la Matriz Agrupa Candidatos Aislados y de la Matriz Candidatos Únicos. El criterio para cada celda son:

 

La ecuación, para una celda NX, es:

= SI(NX_MACA=0;SI(NX_MCU=” “;” “;NX_MCU);NX_MACA)

Donde:

• NX_MACA: Es la misma posición en la Matriz Agrupa Candidatos Aislados
• NX_MCU: Es la misma posición en la Matriz Candidatos Únicos

Para el ejemplo, la Matriz Presenta Soluciones, sería:

Esquema en Excel

Descarga esta plantilla para resolver SUDOKUS en Excel

En el siguiente enlace podrás descargar esta plantilla para resolver SUDOKUS en Excel.

[sociallocker]

Solved_ Sudokus

[/sociallocker]